*relaciones y funciones

En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.

Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.

De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones son funciones.

También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.

Todas las Relaciones pueden ser graficadas en el Plano Cartesiano. 

 

*variable 

Una variable es un elemento de una fórmula, proposición o algoritmo, que puede ser sustituido o puede adquirir un valor cualquiera dentro de su universo. Los valores de una variable pueden definirse dentro de un rango o estar limitados por condiciones de pertenencia.

Puede hablarse de distintos tipos de variable: las variables dependientes, que son aquellas que dependen del valor que asuman otros fenómenos o variables; las variables independientes, cuyos cambios en los valores determinan cambios en los valores de otra; variables cualitativas, que expresan distintas cualidades, características o modalidades; y variables cuantitativas, que se enuncian mediante cantidades numéricas, entre otras.

Por ejemplo: x es una variable del universo {2, 4, 6, 8}. Por lo tanto, x puede tener cualquiera de dichos valores, es decir que puede ser reemplazada por cualquier número par menor a 9.

¿que es una relacion?

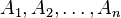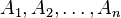Una relación , de los conjuntos es un subconjunto del producto cartesiano

Una relación binaria es una relación entre dos conjuntos.

El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.

Un caso particular es cuando todos los conjuntos de la relación son iguales: en este caso se representa como , pudiéndose decir que la relación pertenece a A a la n.

tipos de relaciones

En las relaciones se diferencian los tipos según el número de conjuntos en el producto cartesiano, que es el número de términos de la relación:

Relación unaria: un solo conjunto

Relación binaria: con dos conjuntos

Relación ternaria: con tres conjuntos

Relación cuaternaria: con cuatro conjuntos

Relación n-aria: caso general con n conjuntos

funcion 
 

• Función matemática - una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el codominio) de forma que a cada elemento del dominio le corresponde un único elemento del codominio.
• Función química - un conjunto de substancias con características semejantes.
•  

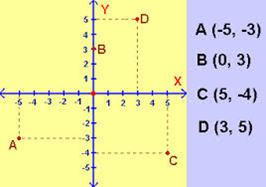
•¿Que es el plano cartesiano?

•El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

¿Cuál es el eje de las axisas?

•El eje de abscisas o eje X es el eje horizontal de un sistema de coordenadas cartesianas.

¿a quien se le llama el padre de la geometría analítica?

René Descartes1 (La Haye, Turena francesa, 31 de marzo de 1596 -Estocolmo, Suecia, 11 de febrero de 1650), también llamado Renatus Cartesius, fue un filósofo, matemático y físico francés, considerado como el padre de la geometría analítica y de la filosofía moderna, así como uno de los nombres más destacados de la revolución científica.

 

•Distancia entre dos puntos

Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas.

Ejemplo: La distancia entre los puntos (-4,0) y (5,0) es 4 + 5 = 9 unidades.

Cuando los puntos se encuentran ubicados sobre el eje y o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.

Ahora si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

Para demostrar esta relación se deben ubicar los puntos A(x1,y1) y B(x2,y2) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa AB y emplear el teorema de pitágoras.

Ejemplo: Calcula la distancia entre los puntos A(7,5) y B (4,1)

d = 5 unidades

ejemplos

•Definición de lugar geométrico 

•

Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad.

La propiedad geométrica que define el lugar geométrico, tiene que traducirse a lenguaje algebraico de ecuaciones.

Ejemplos de lugares geométricos

mediatriz

 La mediatriz de un segmento es la línea recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como el lugar geométrico — la recta — cuyos puntos son equidistantes a los extremos del segmento. También se le llama simetral.

La recta r es la mediatriz del segmento AB. Cualquier punto (P) de ella, equidista de los extremos del segmento A y B (AP = BP).

recta

•En geometría euclidiana, la recta o la línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, es decir, no posee principio ni fin.

•Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición solo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.

•

•En geometría analítica las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano cartesiano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.

  tipos de recta

•Línea Recta: Una cierta cantidad de puntos situados cada uno junto al otro, en una misma dirección, dan origen a un trazo continuo, que es una línea.

•Rectas Secantes: Están conformadas por dos líneas rectas que se unen por un solo punto, lo que hace que estas solo se corten una vez.

•Recta Paralela: Las rectas paralelas son dos líneas rectas ubicadas en el mismo plano que nunca se cortan y no tienen ningún punto en común, cuando los puntos de ambas se ubican a una misma distancia, estas pueden estar rectas o inclinadas.

•Rectas Coincidentes: Las rectas coincidentes son dos líneas rectas que se ubican en un mismo plano, tienen todos sus puntos en común, es decir, se ubican una sobre la otra, tienen la misma dirección; al igual que toda recta se identifica con una letra minúscula.

•Recta Perpendicular: La rectas perpendiculares son aquellas dos líneas rectas que cuando se cortan forman cuatro ángulos iguales; son aquellas líneas que forman un Angulo de noventa grados (90º).

pendiente

•En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento ideal, natural o constructivo respecto de la horizontal.

•En geometría, puede referirse a la pendiente de la ecuación de una recta como caso particular de la tangente a una curva, en cuyo caso representa la derivada de la función en el punto considerado, y es un parámetro relevante, por ejemplo, en el trazado altimétrico de carreteras, vías férreas o canales.

formula de la pendiente

 La pendiente de una recta en un sistema de representación rectangular (de un plano cartesiano), suele estar representada por la letra , y está definida como la diferencia en el eje Y dividido por la diferencia en el eje X para dos puntos distintos en una recta. En la siguiente ecuación se describe:

 

Ecuación de la recta 

La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).

La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.

El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta.

• 1.– Ecuación general de la recta

•Esta es una de las formas de representar la ecuación de la recta.

•De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano), con abscisas (x) y ordenadas (y). 

Ecuación principal de la recta

Esta es otra de las formas de representar la ecuación de la recta.

•

Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:

•Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).

•Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.

•

Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.

•

Ejemplo: El punto (7, 2) (el 7 en la abscisa x y el 2 en la ordenada y) satisface la ecuación y = x – 5, ya que al reemplazar queda

•

2 = 7 – 5 lo que resulta verdadero.

•

Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce, que se obtiene con la fórmula

•

y = mx + n

•

que considera las siguientes variables: un punto (x, y), la pendiente (m) y el punto de intercepción en la ordenada (n), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).

•

Al representar la ecuación de la recta en su forma principal vemos que aparecieron dos nuevas variables: la m y la n, esto agrega a nuestra ecuación de la recta dos nuevos elementos que deben considerase al analizar o representar una recta: la pendiente y el punto de intercepción (también llamado intercepto) en el eje de las ordenadas (y).

•

Respecto a esto, en el gráfico de la izquierda, m representa la pendiente de la recta y permite obtener su grado de inclinación (en relación a la horizontal o abscisa), y n es el coeficiente de posición, el número que señala el punto donde la recta interceptará al eje de las ordenadas (y).

•Forma simplificada de la ecuación de la recta

•

Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas es (0, b) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma

•y − y1 = m(x − x1)

•y – b = m(x – 0)

•y – b = mx

•y = mx + b

ecuación general de la recta

•La ecuación general de una recta es una expresión de la forma Ax+By+C=0, donde A, B y C son números reales.

•La pendiente de la recta es el coeficiente de la x una vez puesta en forma explícita (es decir, despejada y): 

•By = -Ax-C -> -> la pendiente es: m = -A/B

representacion matematica de la circunferencia

Representación grafica de la circunferencia, parábola, elipse e hipérbola.
Circunferencia:
La circunferencia es una línea curva, plana y cerrada, cuya definición más usual es: Una circunferencia esel conjunto de todos los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro.
A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmentode recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longituddel radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia esel perímetro del círculo cuya superficie contiene.
Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección,perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.
La circunferencia de centro en el origen de coordenadas y radio 1se denomina circunferencia unidad o circunferencia goniométrica. Es una curva plana con infinitos ejes de simetría y sus aplicaciones son muy numerosas.

ejemplos

   

ecuacion caronica de la circunferencia

Ecuación Ordinaria de la Circunferencia

Dados las coordenadas del centro de la circunferencia C(h;k) y el radio "r" de la misma, podemos utilizar la siguiente ecuación para determinar el valor de "y" correspondiente a un valor de "x".

Ejemplo:

Hallar la ecuación de la circunferencia cuyo centro es C(2;6) y con radio r = 4

(x - 2)² + (y - 6)² = 4²

Ecuación Canónica de la Circunferencia

Sean ahora las coordenadas del centro de la circunferencia C(0;0) y el radio "r", podemos utilizar la siguiente ecuación para determinar el valor de "y" correspondiente a un valor de "x".

Ejemplo:

Hallar la ecuación de la circunferencia cuyo centro es el origen y con radio r = 3

x ² + y ² = 3²

Ecuación General de la Circunferencia

Si conocemos el centro y el radio de una circunferencia, podemos construir su ecuacion ordinaria, y si operamos los cuadrados, obtenemos la forma general de la ecuación de la circunferencia, así: Prueba:Ejemplo:

Hallar la ecuación general de la circunferencia con centro C(2;6) y radio r = 4

(x - 2)² + (y - 6)² = 4²

x² - 2(2x) + 2² + y² - 2(6y) + 6² = 4²

x² - 4x + 4 + y² - 12y + 36 = 16

x² + y² - 4x - 12y + 4 + 36 - 16 =0

x² + y² - 4x - 12y + 24 = 0

D = -4 , E = -12 , F = +24

ecuación general de la circunferencia

•La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.

 la parabola

•En matemáticas, una parábola (del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.nota 1 nota 2 Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz,nota 3 y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.

•La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).

formulas de la parabola

•Elementos de la parábola 

Una parábola queda definida por el conjunto de los puntos del plano que equidistan de una recta fija y un punto fijo:

•d(P,D)=d(P,F)

•Elementos de la parábola

•Foco: Es el punto fijo F.

•Directriz: Es la recta fija D.

•Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro p.

•Eje: La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el eje de 

simetría de la parábola.

•Vértice: Es el punto medio entre el foco y la directriz. También se puede ver como el punto de intersección del eje con la parábola.

•Radio vector: Es el segmento que une un punto cualquiera de la parábola con el foco.

tipos de parábolas

parábola existen 5 tipos 

horizontal que abre hacia la izquierda 

horizontal que abre a la derrecha 

viertical que abre hacia la izquierda 

vertilca que abre a la derecha 

parabola que esta rotada 

elipse hay 3 la horizontal, la vertical y la rotada 

prabola hay 3 horizontal vertical y rotada

¿que es una elipse?

La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.

 Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.¹ Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

                                            

Elementos de una elipse

La elipse y algunas de sus propiedades geométricas.

La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:

• El semieje mayor (el segmento C-a de la figura), y
• el semieje menor (el segmento C-b de la figura).

Miden la mitad del eje mayor y menor respectivamente.

Puntos de una elipse

Los focos de la elipse son dos puntos equidistantes del centro, F₁ y F₂ en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor (d(P,F₁)+d(P,F₂)=2a).
Por comodidad denotaremos por PQ la distancia entre dos puntos P y Q.
Si F₁ y F₂ son dos puntos de un plano, y 2a es una constante mayor que la distancia F₁F₂, un punto P pertenecerá a la elipse si se cumple la relación:

donde es la medida del semieje mayor de la elipse.


                                        



                           

 

Ejes de una elipse

El eje mayor, 2a, es la mayor distancia entre dos puntos opuestos de la elipse. El resultado de la suma de las distancias de cualquier punto a los focos es constante y equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos opuestos de la elipse. Los ejes de la elipse son perpendiculares entre sí.






funcion 


En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r². Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.

tipos de funciones